Deriving temperature from a spectrum
A ‘rotational’ temperature is derived from the ratio of any two emission lines with measured intensities In and Im via the equation
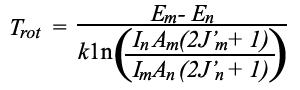
where En and Emare initial rotational state energy levels; Anand Am are transition probabilities; J'n and J'm are upper state, total angular momentum quantum numbers; and k is Planck’s constant.
Analysis calibrations and corrections
Analysis techniques have been developed to optimize the accuracy of the rotational temperature determinations using ratios of the intensities of the spectral lines in the OH(6–2) band denoted P1(2), P1(4) and P1(5). Precise calibration of the Czerny-Turner spectrometer’s spectral response is important for long-term trend assessment. Inter-year spectral response variation of less than 0.3% has been achieved. Temperature errors associated with the response calibration amount to 1.5 K for earlier years and less than 0.3 K since 1996.
Emission lines can be modified by auroral and OH satellite line emissions, and by solar (Fraunhofer) and water vapour absorption. P1(3) is rejected from further analysis due to “un-thermalised” contributions from the OH(5–1)P1(12) lines which adversely affect the analysis. A correction is applied to account for the Q1(5) contribution under P1(2). N2 1PG and N2+ auroral emissions as well as solar Fraunhofer absorption are accounted for by appropriate selection of the backgrounds for each line. Water vapour absorption is not found to be significant. Correction factors are also applied to account for the difference in “Lambda-doubling” between the P-branch lines. These are derived from frequency-stabilised laser determinations of the instrument bandwidth (which is 0.15 nm). A technique for time interpolation of sampled branch lines and backgrounds between spectra has also been developed, which reduces the error associated with possible intensity variations in the time taken to scan a spectrum.
There are three sets of published transitions probabilities and they yield a 12 K range in the absolute temperature derived. An experimental investigation of OH(6–2) Q1/P1 and R1/P1 emission intensity ratios, for rotational states up to j'=4.5, was undertaken to determine which set is most suitable for application to the OH(6-2) band.
Application to the spectra
The concepts described above are combined in the analysis that is represented graphically below:
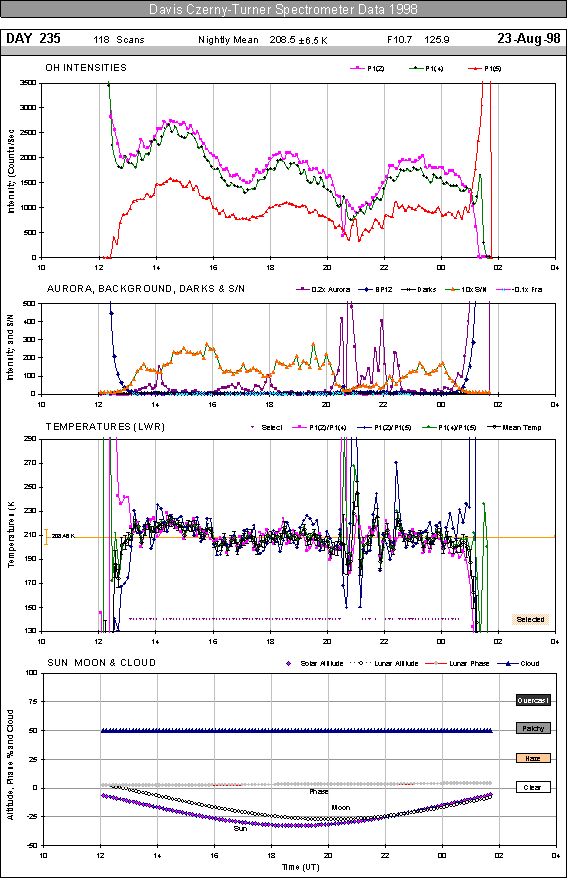
Nightly plots such as the one above are produced for each observing session. The top panel shows variation in P1(2), P1(4) and P1(5) emission intensity over the night. Wave structure with period 3–5 hours are often observed. An auroral activity indicator, mean background level, dark count rate, signal-to-noise and a Fraunhofer absorption index are all plotted in the second panel. Signal-to-noise is calculated as the average of the three P-branch line intensities divided by the average of their background samples.
Temperatures for each possible ratio of the intensities in the top panel, and weighted mean temperature with the maximum of the weighted counting error and weighted standard deviation as error bars, are shown in the third panel.
Selection criteria are applied to reject spectra that do not yield consistent temperatures for each of the three possible ratios, suffer low signal-to-noise, or are contaminated by strong aurora, scattered moonlight or changing cloud conditions. Dots along the bottom of this plot indicate whether a particular temperature result passes all selection criteria. A nightly mean value is calculated from the accepted values solar altitude, lunar altitude and phase, and cloud cover (coded from visual observations and auroral imager video-tape) are also plotted in the bottom panel. Daily F10.7cm solar flux in the header is the observed value from the Canadian National Research Council.
